Collaborative game specification: arriving at common models in bargaining

6 March 2021 by Jesse Clifton

Conflict is often an inefficient outcome to a bargaining problem. This is true in the sense that, for a given game-theoretic model of a strategic interaction, there is often some equilibrium in which all agents are better off than the conflict outcome. But real-world agents may not make decisions according to game-theoretic models, and when they do, they may use different models. This makes it more difficult to guarantee that real-world agents will avoid bargaining failure than is suggested by the observation that conflict is often inefficient.

In another post, I described the "prior selection problem", on which different agents having different models of their situation can lead to bargaining failure. Moreover, techniques for addressing bargaining problems like coordination on solution concepts or surrogate goals / safe Pareto improvements seem to require agents to have a common, explicit game-theoretic model.

In this post, I introduce collaborative game specification (CGS), a family of techniques designed to address the problem of agents lacking a shared model. In CGS, agents agree on a common model of their bargaining situation and use this to come to an agreement. Here is the basic idea:

Two agents are playing an unknown game. They each have private models of this game. (These may be explicit models, as in model-based reinforcement learning, or models implicit in a black-box policy which can be extracted.) By default, they will use these models to make a decision. The problem is that their models may differ, possibly leading to bad outcomes and precluding the use of bargaining protocols which require a shared, explicit model.

Rather than using these default strategies, agents agree on a common model, talk, and use this model to reach an agreement.

Of course, when agreeing on a common model, agents must handle incentives for their counterparts to deceive each other. In the toy illustration below, we’ll see how handling incentives to misrepresent one’s model can be handled in a pure cheap-talk setting.

How might we use CGS to reduce the risks of conflict involving powerful AI systems? One use is to provide demonstrations of good bargaining behavior. Some approaches to AI development may involve training AI systems to imitate the behavior of some demonstrator (e.g., imitative amplification), and so we may need to be able to provide many demonstrations of good bargaining behavior to ensure that the resulting system is robustly able and motivated to bargain successfully. Another is to facilitate bargaining between humans with powerful AI tools, e.g. in a comprehensive AI services scenario.

Aside from actually implementing CGS in AI systems, studying protocols of this kind can give us a better understanding of the limits on agents’ ability to overcome differences in their private models. Under the simple version of CGS discussed here, because agents have to incentivize truth-telling by refusing to engage in CGS sometimes, agents will fail to agree on a common model with positive probability in equilibrium.

I will first give a toy example of CGS (Section 1), and then discuss how it might be implemented in practice (Section 2). I close by discussing some potential problems and open questions for CGS (Section 3). In the Appendix, I discuss a game-theoretic formalism in which CGS can be given a more rigorous basis.

Contents
1 Toy illustration
2 Implementation
3 Questions and potential problems
Appendix: Policy training and deployment as a Bayesian game
References

1 Toy illustration

For the purposes of illustration, we’ll focus on a pure cheap-talk setting, in which agents exchange unverifiable messages about their private models. Of course, it is all the better if agents can verify aspects of each others' private models. See Shin (1994) for a game-theoretic setting in which agents can verifiably disclose (parts of) their private beliefs. But we will focus on cheap talk here. A strategy for specifying a common model via cheap talk needs to handle incentives for agents to misrepresent their private models in order to improve their outcome in the resulting agreement. In particular, agents will need to follow a policy of refusing to engage in CGS if their counterpart reports a model that is too different from their own (and therefore evidence that they are lying). This kind of strategy for incentivizing honesty in cheap-talk settings has been discussed in the game theory literature in other contexts (e.g., Gibbons 1988; Morrow 1994).

For simplicity, agents in this example will model their situation as a game of complete information. That is, agents by default assume that there is no uncertainty about their counterpart’s payoffs. CGS can also be used for games of incomplete information. In this case, agents would agree on a Bayesian game with which to model their interaction. This includes agreement on a common prior over the possible values of their private information.

The "noisy Chicken" game is displayed in Table 1.

In this game, both agents observe a random perturbation of the true payoff matrix of the game. Call agent $i$ 's observation $G_i$ . This might be a world-model estimated from a large amount of data. The randomness in the agents' models can be interpreted as agents having different ways of estimating a model from data, yielding different estimates (perhaps even if they have access to the same dataset). While an agent with more computational resources might account for the fact that their counterpart might have a different model in a fully Bayesian way, our agents are computationally limited and therefore can only apply relatively simple policies to estimated payoff matrices. However, their designers can simulate lots of training data, and thus construct strategies that implicitly account for the fact that other agents may have different model estimates, while not being too computationally demanding. CGS is an example of such a strategy.

A policy will map observations $G_i$ to a probability distribution over $\{ C, D \}$ . We assume the following about the agents' policies:

The agents have default policies 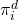$\pi_i^d$ which play according to the (utilitarian)
welfare-optimal Nash equilibrium of their observed game. (Note that CGS does not require that a welfare-optimal Nash equilibrium be played; this is chosen for the purposes of illustration.)
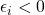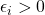So, if $\epsilon_i < 0$ , agent $i$ plays according to $(C, D)$ , and if $\epsilon_i > 0$ , they play according to 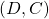$(D, C)$ . Thus they will play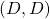 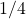$(D, D)$ $1/4$ of the time when each plays according to their default policy.

The agents can instead choose to engage in cheap talk. We will restrict their cheap talk policies to those which implement CGS.

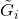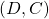Each agent has a reporting policy that maps observations $G_i$ to reported observations $\tilde{G}_i$ . To keep things simple, these reporting policies only distort the observed value of agent $1$ 's payoff at $(D, C)$ by an amount 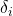$\delta_i$ in a direction that favors them;

Each agent agrees to play according to a combined game if and only if 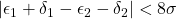$\lvert \epsilon_1 + \delta_1 - \epsilon_2 - \delta_2 \rvert < 8 \sigma$ . This is to disincentivize their counterpart from reporting models that are too different from their own, and therefore likely to be distorted. (I chose 8 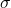$\sigma$ by fiddling around; in practice, the training regime would optimize over cutoff values, too.);

If the agents agree to combine the reported games, they simply take the average of their reported payoff matrices and play the welfare-optimal Nash equilibrium of the resulting game.

Now, we imagine that the agents are AI systems, and the AI developers ("principals") have to decide what policy to give their agent. If their agent is going to use CGS, then they need to train it to use a distortion which is (in some sense) optimal. Thus I will consider the choice of policy on part of the *principals* as a game, where the actions correspond to distortions to use in the distortion policy, and payoffs correspond to the average payoffs attained by the agents they deploy. Then I'll look at the equilibria of this game. This is of course a massive idealization - AI developers will not get together and choose agents whose policies are in equilibrium with respect to some utility functions. The point is only to illustrate how principals might rationally train agents to arrive at a common model under otherwise idealized circumstances.

I ran 1000 replicates of an experiment which computed actions according to the default policies and according to reporting policy profiles with $\sigma=0.5$ and distortions $\delta_1, -\delta_2 \in \{0, \sigma/3, 2 \sigma/3, \sigma\}^2$ . This The payoffs under the default policy profile and the Nash equilibrium (it happened to be unique) of the game in which principals choose the distortion levels $\delta_1, \delta_2$ for their agents are reported in Table 3.

2 Implementation

In practice, CGS can be seen as accomplishing two things:

Providing an inductive bias in the huge space of bargaining strategies towards those which we have reason to think will reduce the risks of bargaining failure from agents having differing models;

Allowing agents to use bargaining strategies which require them to agree on an explicit game-theoretic model, by furnishing unexploitable methods for agreeing on such a model.

Here is how it could be implemented:

1. Take whatever class of candidate policies and policy learning method you were going to use by default. Note that this class of policies need not be model-based, so long as transparency tools can be applied to extract a model consistent with the policies' behavior (see below);

2. Augment the space of policies you are learning over with those that implement CGS. These policies will be composed of

A policy for reporting a (possibly distorted) private model to one's counterpart. For instance, these models might be partially observable stochastic games which model the evolution of some relevant part of the world under different policy profiles the agents could agree to, (perhaps with a prior over each agent's utility function);

A set of acceptable model combination methods;

A policy for deciding whether to accept the other agent's reported model; and play according to the resulting combined game, or reject and play some default policy;

A set of acceptable solution concepts to apply to the combined game (e.g., welfare-optimal Nash equilibrium for some welfare function).

3. Use your default policy learning method on this augmented space of policies.

For example, in training that relies on imitation learning, a system could be trained to do CGS by having the imitated agents respond to certain bargaining situations by offering to their counterpart to engage in CGS; actually specifying an explicit model of their strategic situation in collaboration with the counterpart; and (if the agents succeed in specifying a common model) applying some solution concept to that model in order to arrive at an agreement.

A major practical challenge seems to be having imitated humans strategically specify potentially extremely complicated game-theoretic models. In particular, one challenge is specifying a model at all, and another is reporting a model such that the agent expects in some sense to be better off in the solution of the model that results from CGS than they would be if they used some default policy. The first problem — specifying a complicated model in the first place — might be addressed by applying model extraction techniques to some default black box policy in order to infer an explicit world-model. The second problem — learning a reporting policy which agents expect to leave them better off under the resulting agreement — could be addressed if different candidate reporting policies could be tried out in a high-quality simulator.

3 Questions and potential problems

One issue is whether CGS could actually make things worse. The first way CGS could make things worse is via agents specifying models in which conflict happens in equilibrium. We know that conflict sometimes happens in equilibrium. Fearon (1995)'s classic rationalist explanations for war show how war can occur in equilibrium due to agents having private information about their level of strength or resolve that they are not willing to disclose, or agents not being able to credibly commit to not launching preemptive attacks when they expect that their counterpart will gain strength in the future. Likewise, threats and punishments can be executed and equilibrium for reasons of costly signaling (e.g., Sechser 2010) or falsely detected defections (e.g., Fudenberg et al. 2009). A related issue is that it is not clear how the interaction of CGS and model misspecification affects its safety. For instance, agents who underestimate the chances of false detections of nuclear launches may place nuclear weapons on sensitive triggers, incorrectly thinking that nuclear launch is almost certain not to occur in equilibrium.

The second way training agents to do CGS could make things worse is by encouraging them to use dangerous decision procedures outside of CGS. The problems associated with designing agents to maximize a utility function are well-known in AI safety. Depending on how agents are trained to do CGS, it may make them more likely to make decisions in situations other than bargaining situations via expected utility maximization. For instance, training agents to do CGS may produce modules that help agents to specify a world-model and utility function, and maximize the expectation of that utility function, and agents may use the modules when making decisions in non-CGS contexts.

In light of this, we would want to make sure CGS preserves nice properties that a system already has. CGS should be *alignment-preserving*: intuitively, modifying a system's design to implement CGS shouldn't make misalignment more likely. CGS should also preserve properties like *myopia*: modifying a myopic system to use CGS shouldn't make it non-myopic. Importantly, ensuring the preservation of properties other than alignment which make catastrophic bargaining failure less likely may help to avoid worst-case outcomes even if alignment fails.

Finally, there is the problem that CGS still faces equilibrium and prior selection problems. (See the Appendix for a formulation of CGS in the context of a Bayesian game; such a game assumes a common prior — in this case, a prior arising from the distribution of environments on which the policies are trained — and will, in general, have many equilibria.) Thus there is a question of how much we can expect actors to coordinate to train their agents to do CGS, and how much CGS can reduce risks of bargaining failure if AI developers do not coordinate.

Appendix: Policy training and deployment as a Bayesian game

As in the toy illustration, we can think of agents' models as private information, drawn from some distribution that depends on the (unknown) underlying environment. Because agents are boundedly rational, they can only reason according to these (relatively simple) private models, rather than a correctly-specified class of world-models. However, the people training the AI systems can generate lots of training data, in which agents can try out different policies for accounting for the variability in their and their counterpart's private models. Thus we can think of this as a Bayesian game played between AI developers, in which the strategies are policies for mapping private world-models to behaviors. These behaviors might include ways of communicating with other agents in order to overcome uncertainty, which in turn might include CGS. The prior for this Bayesian game is the distribution over private models induced by the training environments and the agents' model-learning algorithms (which we take to be exogenous for simplicity).

As I noted above, this Bayesian game still faces equilibrium and prior selection problems between the AI developers themselves. It also makes the extremely unrealistic assumption that the training and deployment distributions of environments are the same. The goal is only to clarify how developers could (rationally) approach training their agents to implement CGS under idealized conditions.

Consider two actors, who I will call "the principals'', who are to train and deploy learning agents. Each principal $i$ has utility function $u_i$ . The game that the principals play is as follows:

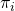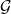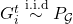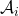The principals train policies $\pi_i$ on independent draws from a distribution of multi-agent environments (for instance, stochastic games) taking values in $\mathcal{G}$ , $G^t_{i} \overset{\mathrm{i.i.d}}{\sim} P_{\mathcal{G}}$ for $i=1,2$ . These environments represent the environments in which the agents are trained and deployed. Policies return actions in the spaces $\mathcal{A}_i$ . (Note that, in sequential environments — e.g., stochastic games — these "actions'' may in fact be policies mapping, e.g., the states of stochastic game to actions in that stochastic game.)

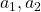For each environment $G$ , a function mapping pairs of actions $a_1, a_2$ to each principal $i$ 's payoffs, $u_i(a_1, a_2; G)$ ;

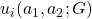In each training environment, agents receive private observations 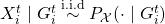$X^t_{i} \mid G_{i}^t \overset{\mathrm{i.i.d}}{\sim} P_{\mathcal{X}}(\cdot \mid G^t_{i})$ on which they can condition their policies, with 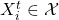$X_i^t \in \mathcal{X}$ . These observations will correspond to data from which the agents estimate world-models (e.g., a model of a stochastic game) or form beliefs about other agents' private information.

The agents are deployed and take actions in an environment 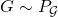$G \sim P_{\mathcal{G}}$ based on private information $X_i \sim P_{\mathcal{X}}(\cdot \mid G)$ .

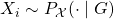The choice of what policy to deploy is a game with strategies $\pi_1, \pi_2$ and ex ante payoffs

$u_i(\pi_1, \pi_2) = \int u_i\left\{ \pi_1(X_1), \pi_2(X_2); G\right\} \mathrm{d} P_{\mathcal{X}}(X_1 \mid G) \mathrm{d}P_{\mathcal{X}}(X_2 \mid G) \mathrm{d}P_{\mathcal{G}}(G).$

We will for now suppose that during training the value of policy profiles $(\pi_1, \pi_2)$ under each utility function in $\mathcal{U}_i$ can be learned with high accuracy.

How should a principal choose which policy to deploy? In the absence of computational constraints, a natural choice is Bayesian Nash equilibrium (BNE). In practice, it will be necessary to learn over a much smaller class of policies than the space of all maps. Let $\Pi_1, \Pi_2$ be sets of policies such that it is tractable to evaluate each profile $\pi_1, \pi_2 \in \Pi_1 \times \Pi_2$ . In this context, assuming that the principals' utility functions are common knowledge, a pair of policies $\pi_1, \pi_2$ is a BNE if it satisfies for $i=1,2$ (indexing $i$ 's counterpart by $j$ )

$\begin{aligned} & \int u_i\{ \pi_i(X_i), \pi_j(X_j); G \} \mathrm{d} P_{\mathcal{X}}(X_i \mid G) \mathrm{d}P_{\mathcal{X}}(X_j \mid G) \mathrm{d}P_{\mathcal{G}}(G) \\ & \quad \geq \int u_i\{ \pi'_i(X_i), \pi_j(X_j); G \} \mathrm{d} \mathrm{d} P_{\mathcal{X}}(X_i \mid G) \mathrm{d}P_{\mathcal{X}}(X_j \mid G) \mathrm{d}P_{\mathcal{G}}(G), \text{ for all } \pi'_i \in \Pi_i. \end{aligned}$

When $\Pi_i$ consists of policies with limited capacity (reflecting computational boundedness), agents may learn policies which do not account for the variability in the estimation of their private models. I will call the class of such policies learned over during training time the "default policies'' $\Pi_i^d$ . To address this problem in a computationally tractable way, we introduce policies $\Pi_i^{\mathrm{cgs}}$ which allow for the specification of a shared model of $G$ . Let $\widetilde{\mathcal{G}}$ be a set of models, and let $\mathcal{Y}$ be a set of solution concepts which map elements of $\widetilde{\mathcal{G}}$ to (possibly random) action profiles. In the toy illustration, agents specified models in the set $\widetilde{\mathcal{G}}$ of $2 \times 2$ bimatrices, and the solution concept they used was the Nash equilibrium which maximized the sum of their payoffs in the game $\widetilde{G}$ .

Then, the policies $\pi_i \in \Pi_i^{\mathrm{cgs}}$ have the property that, for some $\pi_j \in \Pi_j^{\mathrm{cgs}}$ , the policy profile $\pi = (\pi_i, \pi_j)$ succeeds in collaboratively specifying a game with positive probability. That is, with positive probability we have $\pi(X_1, X_2) = y(\widetilde{G})$ for some $y \in \mathcal{Y}$ and some $\widetilde{G} \in \widetilde{\mathcal{G}}$ .

The goal of principals who want their agents to engage in collaborative game specification is to find a policy profile in $\Pi^{\mathrm{cgs}}$ which is a Bayes-Nash equilibrium that improves upon any equilibrium in $\Pi_1^d \times \Pi_2^d$ and which succeeds in collaboratively specifying a game with high probability.

Now, this model is idealized in a number of ways. I assume that the distribution of training environment $P_{\mathcal{G}}$ matches the distribution of environments encountered by the deployed policies. Moreover, I assume that both principals train their agents on this distribution of environments. In reality, of course, these assumptions will fail. A more modest but attainable goal is to use CGS to construct policies which perform well on whatever criteria individual principals use to evaluate policies for multi-agent environments, as discussed in the Section 2 (Implementation).

References

James D Fearon. Rationalist explanations for war. International organization, 49(3):379–414, 1995.

Drew Fudenberg, David Levine, and Eric Maskin. The folk theorem with imperfect public information. In A Long-Run Collaboration On Long-Run Games, pages 231–273. World Scientific, 2009.

Robert Gibbons. Learning in equilibrium models of arbitration. Technical report, National Bureau of Economic Research, 1988.

James D Morrow. Modeling the forms of international cooperation: distribution versus information. International Organization, pages 387–423, 1994.

Todd S Sechser. Goliath’s curse: Coercive threats and asymmetric power. International Organization, 64(4):627–660, 2010.

Hyun Song Shin. The burden of proof in a game of persuasion. Journal of Economic Theory, 64(1):253–264, 1994.